1. 问题
通过修改法向量达到修改光强的效果。假设原法向量为\(n\),光照方向为\(D\),对应原光强\(L_0 = n\cdot D\)。现在希望通过叠加法向量\(\delta n\)达到修改光强\(\delta L\)。
2. 原理
对应求解以下的方程
$$
\begin{split}
\frac{(n + \delta n)\cdot D}{\| n + \delta n\|} &= L_0 + \delta L\\
\frac{\delta n \cdot D}{\| n + \delta n\|} &= \delta L ~~(\text{since}~n\cdot D = L_0)
\end{split}
$$
方程欠定。添加约束\(\| n + \delta n\| = 1\),方程拆解为
$$
\delta n \cdot D = \delta L ~~(\text{超平面方程})\\
\| n + \delta n\| = 1 ~~(\text{球方程})
$$
说明方程组的解集为超平面和球的交集(圆、点、空集),依然欠定。设超平面的切向量为\(\tau_1\),\(\tau_2\),则
$$
\delta n = \delta L \cdot D + k_1 \tau_1 + k_2 \tau_2 \\
n = \underset{=L_0}{(n\cdot D)}D + (n\cdot \tau_1)\tau_1 + (n\cdot \tau_2)\tau_2
$$
于是
$$
(L_0+\delta L)^2 + (n\cdot \tau_1+k_1)^2 + (n\cdot \tau_2+k_2)^2 = 1 \\
(n\cdot \tau_1+k_1)^2 + (n\cdot \tau_2+k_2)^2 = 1-(L_0+\delta L)^2
$$
当\(L_0 + \delta L < 1\),令\(r^2 =1 -(L_0 + \delta L)^2 > 0\),转为最优化问题
$$
\min_{k_1,k_2} k_1^2 + k_2^2\\s.t.~(n\cdot \tau_1+k_1)^2 + (n\cdot \tau_2+k_2)^2=r^2
$$
几何上,相当于计算坐标原点到圆的最小距离\(d_m\)。圆心坐标\(C=(-n\cdot \tau_1,-n\cdot \tau_2)\),半径为\(r\)。令\(d\)为坐标原点到圆心的距离
$$
d_m = |d-r|
$$
对应的坐标
$$
(k_1^*,k_2^*) = d_m \cdot C
$$
当\(L_0 + \delta L = 1\),方程右边为零,可以求出唯一解
$$
k_1 = - n \cdot \tau_1, ~k_2 = -n \cdot \tau_2
$$
用极限的思想,\(r \rightarrow 0^+\),此时有\(d_m \rightarrow d\),\(\delta L = 1 - L_0\),继续使用表达式\((k_1^*,k_2^*) = d_m \cdot C\)作为最优解可保证连续性。
当\(L_0 + \delta L > 1\),说明已经超过最大光强,不可实现,所以采用\(L_0 + \delta L = 1\)情形下的解。
 Charlie小站
Charlie小站
 用C语言画颗心(一)——心形曲面
用C语言画颗心(一)——心形曲面 单位速度参数化
单位速度参数化 procrustes分析原理与应用
procrustes分析原理与应用 用C语言画颗心(三)——着色
用C语言画颗心(三)——着色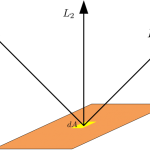 用C语言画颗心(二)——光照模型
用C语言画颗心(二)——光照模型 三门问题(Monty Hall problem)
三门问题(Monty Hall problem)
评论前必须登录!
登陆 注册